基础

Last updated Dec 12, 2021

# 基础

episode：从一个游戏开始到结束，叫做一个episode

loss:可以作为负的reward

Monte-Carlo(MC):

# 分类

是否理解环境？
不理解环境：不尝试去理解环境，环境给什么就是什么 Model-free
理解环境：为真实世界建模 Model-based
Model-based 就是在model free的基础上多一个虚拟环境
基于Policy-Based与基于Value-Based
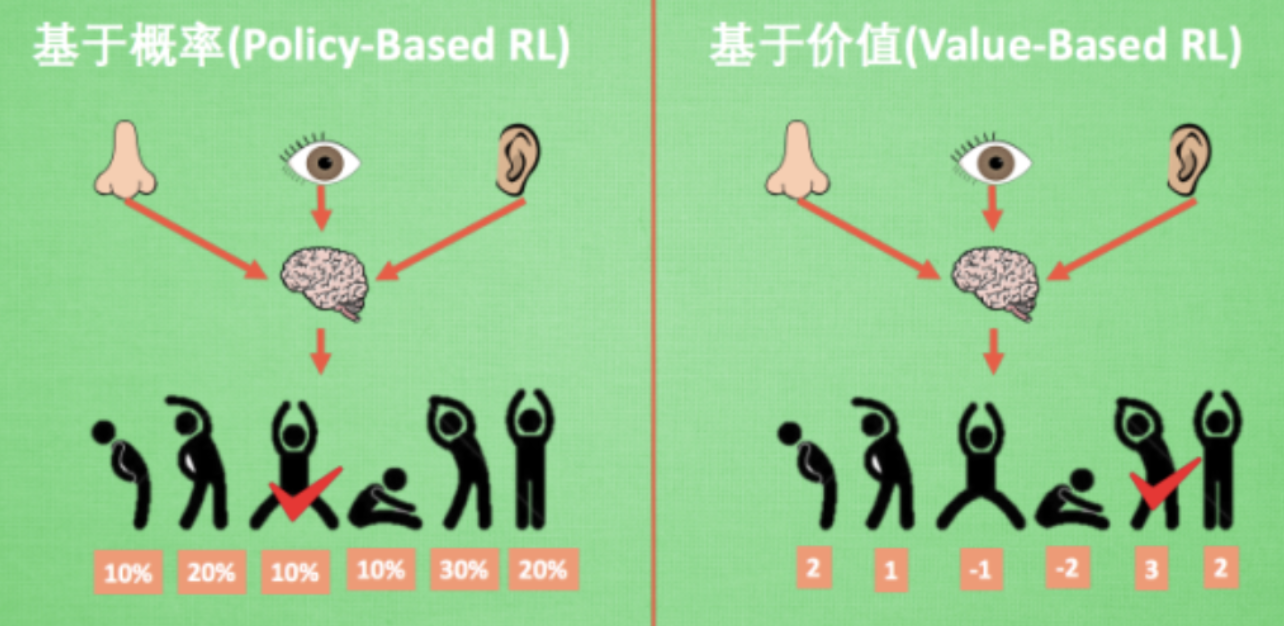
基于概率：直接输出下一步要采取动作的概率，根据概率选取行动，可以支持连续动作 Policy Gradients
基于价值（连续动作无能为力）：而基于价值的方法输出则是所有动作的价值, 根据最高价值来选着动作 Q-Learning Sarsa
基于价值的谁价值高选谁，基于概率根据概率执行动作
更新
回合更新：回合结束后更新行为准则基础Policy Gradients Monte-carlo Learning
单步更新：每一步都更新准则 Q-Learning Sarsa 升级版Policy Gradients
在线与否
在线学习边玩边学，sarsa、sarsa(lambda)
离线学习学完再玩，Q Learning、Deep Q Network

现在，如果我们知道MDP中的所有东西，那么我们可以不用在环境中做出动作便可直接求解，我们通常称在执行动作前作出的决策为规划(planning)，那么一些经典的规划算法能够直接求解MDP问题，包括值迭代和策略迭代等。

那么，当agent不知道转移概率函数TT和奖励函数RR，它是如何找到一个好的策略的呢，当然会有很多方法：

# Model-based RL

一种方法就是Model-based方法，让agent学习一种模型，这种模型能够从它的观察角度描述环境是如何工作的，然后利用这个模型做出动作规划，具体来说，当agent处于s1s1状态，执行了a1a1动作，然后观察到了环境从s1s1转化到了s2s2以及收到的奖励rr, 那么这些信息能够用来提高它对T(s2|s1,a1)T(s2|s1,a1)和R(s1,a1)R(s1,a1)的估计的准确性，当agent学习的模型能够非常贴近于环境时，它就可以直接通过一些规划算法来找到最优策略，具体来说：当agent已知任何状态下执行任何动作获得的回报，即R(st,at)R(st,at)已知，而且下一个状态也能通过T(st+1|st,at)T(st+1|st,at)被计算，那么这个问题很容易就通过动态规划算法求解，尤其是当T(st+1|st,at)＝1T(st+1|st,at)＝1时，直接利用贪心算法，每次执行只需选择当前状态stst下回报函数取最大值的动作(maxaR(s,a|s=st)maxaR(s,a|s=st))即可，这种采取对环境进行建模的强化学习方法就是Model-based方法

# Model free RL

但是，事实证明，我们有时候并不需要对环境进行建模也能找到最优的策略，一种经典的例子就是Q-learning，Q-learning直接对未来的回报Q(s,a)Q(s,a)进行估计，Q(sk,ak)Q(sk,ak)表示对sksk状态下执行动作atat后获得的未来收益总和E(∑nt=kγkRk)E(∑t=knγkRk)的估计，若对这个Q值估计的越准确，那么我们就越能确定如何选择当前stst状态下的动作：选择让Q(st,at)Q(st,at)最大的atat即可，而Q值的更新目标由Bellman方程定义，更新的方式可以有TD（Temporal Difference）等，这种是基于值迭代的方法，类似的还有基于策略迭代的方法以及结合值迭代和策略迭代的actor-critic方法，基础的策略迭代方法一般回合制更新（Monte Carlo Update），这些方法由于没有去对环境进行建模，因此他们都是Model-free的方法

所以，如果你想查看这个强化学习算法是model-based还是model-free的，你就问你自己这个问题：在agent执行它的动作之前，它是否能对下一步的状态和回报做出预测，如果可以，那么就是model-based方法，如果不能，即为model-free方法。

# Policy-Based&Value-Based

Policy-Based的方法直接输出下一步动作的概率，根据概率来选取动作。但不一定概率最高就会选择该动作，还是会从整体进行考虑。适用于非连续和连续的动作。常见的方法有policy gradients。

Value-Based的方法输出的是动作的价值，选择价值最高的动作。适用于非连续的动作。常见的方法有Q-learning和Sarsa。

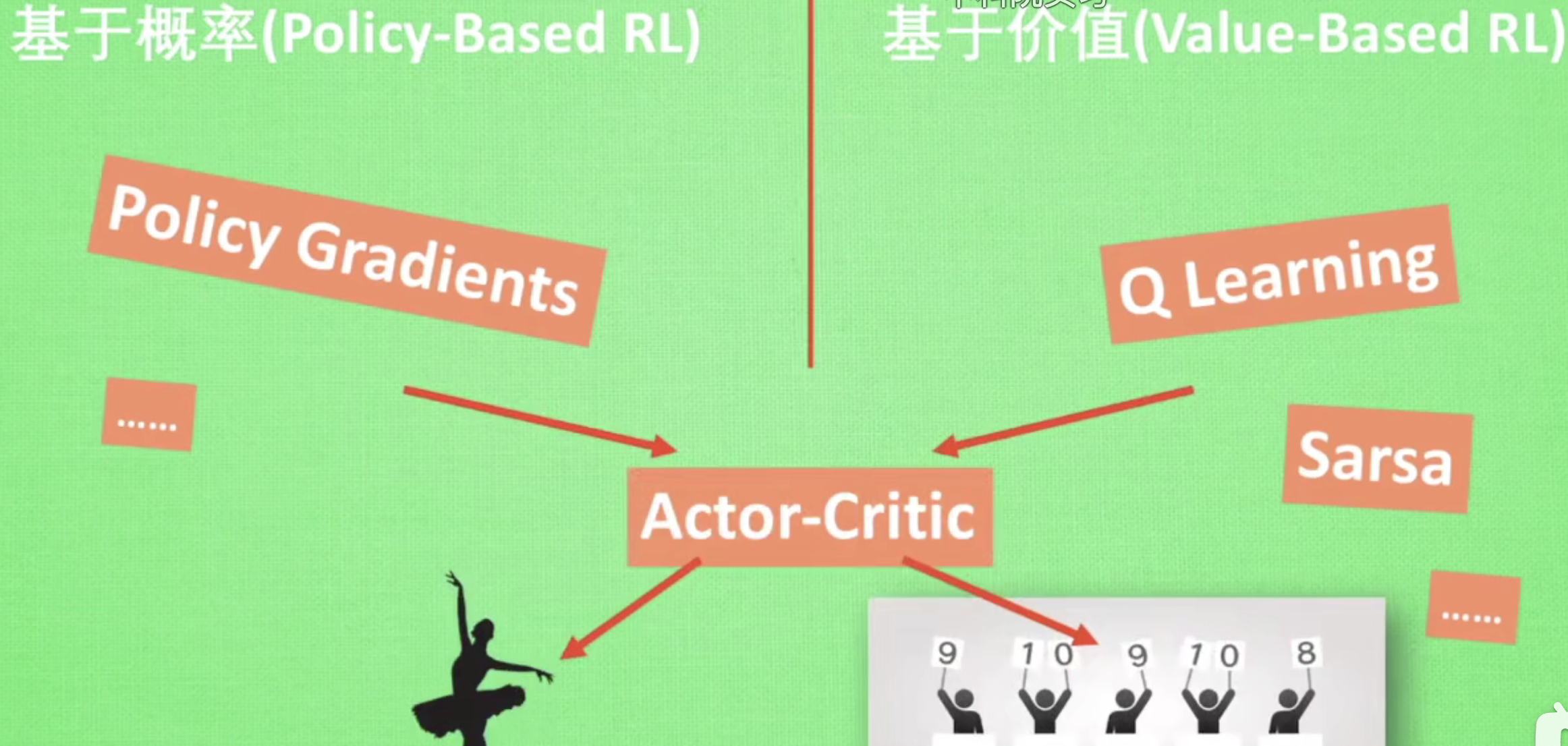
更为厉害的方法是二者的结合：Actor-Critic，Actor根据概率做出动作，Critic根据动作给出价值，从而加速学习过程。

# On-policy&Off-policy

更新值函数时是否只使用当前策略所产生的样本

Q-learning, Deterministic policy gradient是Off-police算法,这是因为他们更新值函数时,不一定使用当前策略$\pi_t$产生的样本. 可以回想DQN算法,其包含一个replay memory.这个经验池中存储的是很多历史样本(包含$\pi_1 ,\pi_2,…,\pi_t$的样本 ),而更新Q函数时的target用的样本是从这些样本中采样而来,因此,其并不一定使用当前策略的样本.

Reinforce, trpo, sarsa都是On-policy,这是因为他们更新值函数时,只能使用当前策略产生的样本.具体的,reinforce的梯度更新公式中 ,这里的R就是整个episode的累积奖赏,它用到的样本必然只是来自于$\pi_t$。

# 算法

# Q-learning

Q-learning算法最主要的就是Q表格,里面存着每个状态的动作价值。然后用Q表格用来指导每一步的动作。并且每走一步,就更新一次Q表格,也就是说用下一个状态的Q值去更新当前状态的Q值。

# DQN

Deep Q Network(DQN)的本质其实是Q-learning算法,改进就是把Q表格换成了神经网络,向神经网络输入状态state,就能输出所有状态对应的动作action。

# Policy Gradient

在讲PG算法前,我们需要知道的是,在强化学习中,有两大类方法,一种基于值（Value-based）,一种基于策略（Policy-based）:

在这里插入图片描述

Value-based的算法的典型代表为Q-learning和SARSA,将Q函数优化到最优,再根据Q函数取最优策略;Policy-based的算法的典型代表为Policy Gradient,直接优化策略函数。

可以举一个例子区分这两种方法:如果用DQN玩剪刀石头布这种随机性很大的游戏,很可能训练到最后,一直输出同一个动作;但是用Policy Gradient的话,优化到最后就会发现三个动作的概率都是一样的。

可以通过类比监督学习的方式来理解Policy Gradient。向神经网络输入状态state,输出的是每个动作的概率,然后选择概率最高的动作作为输出。训练时,要不断地优化概率,尽可能地使输出值的概率逼近1。

# DPG

Deterministic policy gradient(DPG)算法可以理解为PG+DQN,它是首次能处理确定性的连续动作空间问题的算法。要学习DPG算法,就要知道Actor-Critic结构,Actor的前生是Policy Gradient,可以在连续动作空间内选择合适的动作action;Critic的前生是DQN或者其他的以值为基础的算法，可以进行单步更新，效率更高。Actor基于概率分布选择行为,Critic基于Actor生成的行为评判得分,Actor再根据Critic的评分修改选行为的概率。DPG就是在Actor-Critic结构上做的改进,让Actor输出的action是确定值而不是概率分布。