jieye の数字花园

Last updated Unknown

随机选择算在是《算法导论》中一个经典的算法，其时间复杂度为 O(n)，是一个线性复杂度的方法。这个方法并不是所有同学都知道，为了将算法讲透，先聊一些前序知识，一个所有程序员都应该烂熟于胸的经典算法：快速排序。

其核心算法思想是，分治法。分治法（Divide&Conquer），把一个大的问题，转化为若干个子问题（Divide），每个子问题“都”解决，大的问题便随之解决（Conquer）。这里的关键词是“都”。从伪代码里可以看到，快速排序递归时，先通过partition把数组分隔为两个部分，两个部分“都”要再次递归。

分治法有一个特例，叫减治法。减治法（Reduce&Conquer），把一个大的问题，转化为若干个子问题（Reduce），这些子问题中“只”解决一个，大的问题便随之解决（Conquer）。这里的关键词是“只”。

二分查找binary_search，BS，是一个典型的运用减治法思想的算法二分查找，一个大的问题，可以用一个mid元素，分成左半区，右半区两个子问题。而左右两个子问题，只需要解决其中一个，递归一次，就能够解决二分查找全局的问题。

通过分治法与减治法的描述，可以发现，分治法的复杂度一般来说是大于减治法的：

快速排序：O(nlg(n)) > 二分查找：O(lg(n))

话题收回来，快速排序的核心是： i = partition(arr, low, high); 这个partition是干嘛的呢？顾名思义，partition会把整体分为两个部分。更具体的，会用数组 arr 中的一个元素（默认是第一个元素 t=arr[low], 也可以随机选择pivot）为划分依据，将数据 arr[low, high]划分成左右两个子数组：

左半部分，都比t大右半部分，都比t小中间位置i是划分元素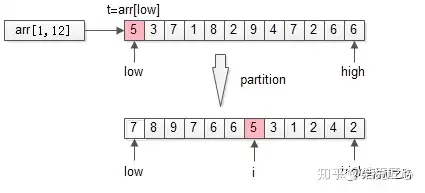以上述TopK的数组为例，先用第一个元素t=arr[low]为划分依据，扫描一遍数组，把数组分成了两个半区：左半区比 t 大右半区比 t 小中间是 t partition 返回的是 t 最终的位置 i。很容易知道，partition 的时间复杂度是 O(n)。

Partition 和 TopK 问题有什么关系呢？ TopK 是希望求出 arr[1, n]中最大的 k 个数，那如果找到了第 k 大的数，做一次 partition，不就一次性找到最大的 k 个数了么？

画外音：即 partition 后左半区的 k 个数。

问题变成了 arr[1, n]中找到第 k 大的数。

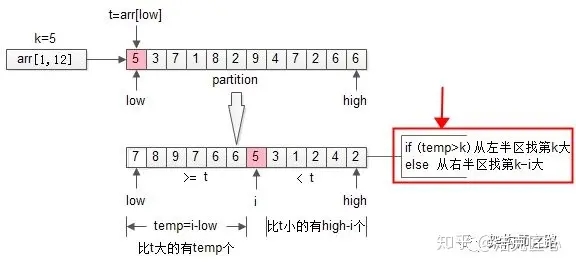
再回过头来看看第一次 partition，划分之后：i = partition (arr, 1, n);

如果 i 大于 k，则说明 arr[i]左边的元素都大于 k，于是只递归 arr[1, i-1]里第 k 大的元素即可；如果 i 小于 k，则说明说明第 k 大的元素在 arr[i]的右边，于是只递归 arr[i+1, n]里第 k-i 大的元素即可；

这就是随机选择算法 randomized_select，RS，其伪代码如下：

1
2
3
4
5
6
7
8
9
int RS(arr, low, high, k){
if(low== high) return arr[low];
i= partition(arr, low, high);
temp= i-low; //数组前半部分元素个数
if(temp>=k)
return RS(arr, low, i-1, k); //求前半部分第k大
else
return RS(arr, i+1, high, k-i); //求后半部分第k-i大
}

这是一个典型的减治算法，递归内的两个分支，最终只会执行一个，它的时间复杂度是 O (n)。再次强调一下：分治法，大问题分解为小问题，小问题都要递归各个分支，例如：快速排序减治法，大问题分解为小问题，小问题只要递归一个分支，例如：二分查找，随机选择通过随机选择（randomized_select），找到 arr[1, n]中第 k 大的数，再进行一次 partition，就能得到 TopK 的结果。

jieye の数字花园

Backlinks

Interactive Graph